Posted by: @derek-m

↑

I think that you will find that the modeling tool already takes account of the variation of COP with load, also with OAT and LWT, by extrapolating the correct values from the manufacturers data.

I fully acknowledge that, I'm just thinking about the problem of doing it in a way that is easier to understand and also perhaps can easily be adapted to other manufacturers heat pumps.  Currently I can't think of one.

Posted by: @derek-m

↑

Table 1 was primarily to illustrate that without recovery boost it may not be possible to fully recover IAT. My calculation of energy saving would be given by 4819/26893 = 17.92%.

Thanks for the explanation, just one supplementary, should we infer from the quote above that you don't consider this a valid scenario in answer to the question posed?

James

Posted by: @jamespa

↑

Posted by: @derek-m

↑

Table 1 was primarily to illustrate that without recovery boost it may not be possible to fully recover IAT. My calculation of energy saving would be given by 4819/26893 = 17.92%.

Thanks for the explanation, just one supplementary, should we infer from the quote above that you don't consider this a valid scenario in answer to the question posed?

 

James

I was merely stating that without some form of recovery boost, the time required for IAT to reach the desired value may be lengthy. A further determining factor is the size of boost and the period over which it is supplied. Just as with the 'slow and low' continuous running regime, a longer slower boost should provide greater energy saving. At the end of the day it is for individual heat pump owners to find out what works best for them, taking all considerations into account.

Posted by: @derek-m

↑

There is no 'black box', there are no hidden cells, everything is open to view.

What I am getting at and what in fact I said was that in effect it becomes a black box, in part because of the complexity of the overall design, but mainly because of the very long complex multi-bracketed formulas, which are very hard to get one's head round. I'm hoping that @jamespa's attempts to improve clarity will bear fruit. I think the complexity does matter, because it hinders attempts by others to verify the code. The verification isn't a snide attempt to catch you out, it is a sensible precautions because we all make mistakes.

Posted by: @derek-m

↑

I would have thought by now that you would have realised that 250kWh is the same as 250000Wh. Please let me know which you prefer.

Of course I know that, and it isn't what I was getting at, which was/is: "what I am asking is why 250kWh?" as in why did you choose 250 rather 500 or 125kWh? This seems an important question, given we agree there appears to be standard way of deriving this figure. I also noted the units in the spreadsheet change (watts/kWh ie sometimes it is power, sometimes it is energy), and furthermore neither appear to be the units used elsewhere, ditto for thermal mass/capacity. We appear to dealing with something that changes its name and units, against a background of that thing having no standard  quantification method, which seems to me be worthy of clarification.

Posted by: @derek-m

↑

If you are not happy with Thermal Mass or Thermal Capacity then please provide a suitable alternative. If you can provide an alternative method of quantifying a building's thermal capacity then please do so.

Again this is not what I said, which was that they appear to be used interchangeably in the spreadsheet, when they are normally considered to be two different things. Very loosely, as I understand it, and I may well have got it wrong, thermal capacity is specific heat of a material, while thermal mass also takes into account how much there is of the material: a ten gallon drum of water has twice the thermal mass of a five gallon drum.

I think I do get the concept, thermal mass can act like a thermal 'battery', or storage heater, but bigger thermal mass comes at a price, slower to warm it up (but also slower to cool down).

Posted by: @derek-m

↑

If you can provide an alternative method of quantifying a building's thermal capacity then please do so.

I thought we'd agreed there isn't one...

Posted by: @derek-m

↑

The values from row 24 are actually used within the table, seek and ye shall find.

I did seek, but didn't find. I even used LibreOffice Calc's Trace Precedents/Dependents and for some unknown the first time it didn't find anything, but I have just run it again, and this time it did: it is used in the formula that calculates the Actual IAT (finish) (row 13), I offer my apologies for missing this first time round.

This formula is interesting: it scales the Actual IAT at the start of the period by the thermal capacity (mass?) currently 'in the bank' divided by the initial thermal capacity (mass?) to derive the Actual IAT at the end of the period (which then logically becomes the start IAT for the next period). The current 'in the bank' thermal capacity (mass?) comes from the current energy in and out 'profit and loss' account, and the net energy can be positive (in which case the scaling factor is greater than one, and the IAT goes up), or negative (in which case the scaling factor is less than one, and the IAT goes down).

What all this seems to suggest to me is that the chosen, but still at the end of the day arbitrary, thermal capacity (mass?) has a definite effect on the IAT (which can be seen by changing it) but I am still stuck with my earlier question: how do we know 250000 is the right number? This number has a pronounced effect on the model results, surely we need to be sure we are using the right number (or a good approximation, with reasons)? 

Notwithstanding what I say above, I remain very impressed by your ability to put together complex spreadsheets.     

Posted by: @jamespa

↑

Posted by: @derek-m

↑

I think that you will find that the modeling tool already takes account of the variation of COP with load, also with OAT and LWT, by extrapolating the correct values from the manufacturers data.

I fully acknowledge that, I'm just thinking about the problem of doing it in a way that is easier to understand and also perhaps can easily be adapted to other manufacturers heat pumps.  Currently I can't think of one.

 

Let me try to explain the various problems, and then you can decide whether to explore this matter further.

The 'Initial Data' sheet contains the data extracted from the Ecodan manual, which is tabulated at various LWT's and various OAT's. Each section is sub-divided, which in the case for the Ecodan, is into four sections, labelled max, nom, mid and min. I did originally create a modeling tool for Midea units, which only have three sub-divisions, so Midea data could easily be used with the present modeling tool, by simply having two sub-divisions with the max data. This should also work with data from other manufacturers provided that their data tables follow a similar format to the Mitsubishi units.

The data tables within the 'Detailed Data' sheet are extrapolated from the initial data, and although I did not do so at the time, could be linked back to the Initial Data, so it would only be necessary to update this sheet for different models and different manufacturers.

The WC Modeling Tool also does not require all the Detailed Data tables, since the underlying data is the same in each table, so only one table would actually be required.

The most important table now is the 'WC Table', which is used to extract the necessary data from the Detailed Data and produce the data required in the 'Play Area'. Whilst many of the formula's used are complex, I feel that they are no more complex than required. If individuals really need to know what is happening within a particular cell I will be happy to explain, but I don't intend to write a detailed manual explaining each 'nut and bolt', when I have clearly stated which cells can be changed and which should not.

The WC table operates in the following manner.

The user can individually set the OAT for any of the 24 one hour periods, which updates the relevant cell in column C of the table. Changing the OAT value also modifies the LWT for each 1 hour slot, with reference to the WC Curve values. The required LWT value is updated in column E of the WC Table.

Changing the OAT value also modifies the Energy Supply value, which in turn updates the relevant cell in column D of the WC table.

Using the OAT, LWT and Energy Supply values, the relevant COP value is extrapolated from the WC Table with the relevant cell in column E being updated. This COP value also updates the relevant cell within the Play Area.

The rest should be fairly easy to understand.

@cathoderay

250kWh was chosen because it provides a believable fall in IAT when the heat pump is stopped. I have tried various values and 250kWh seem to be mid range. Is that acceptable?

If you wish I can hide all the formula's and tables and just present the input and output cells, which is what you would probably get with a commercial modeling tool. Would that be agreeable?

I don't know the Thermal Mass/Capacity of anyone's home, but by trying different values in the modeling tool, I can deduce that a thermal mass of 50kWh would probably lead to a fall of 5C in IAT over a 1 hour period during setback, whilst a thermal mass of 1000kWh would probably take several hours for the IAT to fall 1C.

The value is adjustable, for the precise reason that the thermal mass value needs to matched to the characteristics of the home in question.

Does that answer your question?

Posted by: @derek-m

↑

250kWh was chosen because it provides a believable fall in IAT when the heat pump is stopped. I have tried various values and 250kWh seem to be mid range. 

That's great, it's all I wanted to know, how you got to the number you used. Given there is no standard way to get it, using a number that produces sane falls in the IAT is fine, and we can if we want to factor in that that is how the number was selected.  

Posted by: @cathoderay

↑

Posted by: @jamespa

↑

In the absence of any high probability that we will get a run of days when the OAT profile is identical, enabling a true control experiment to be run, I've been giving some thought to possible experimental techniques to extract the signal from the noise.  Two come to mind, but both require quite a lot of measurement:

Interesting, I will give it some thought. Python is good at automated data collection, and even a goon like me can write the code, given @derek-m's helpful assistance eg in working out how to read binary data.

In the meantime, I was going to ask you another question, if I may, as another way of looking at the question of whether setbacks save energy. It has been touched upon before, but this is if you like a succinct form of the question. Imagine we have three identical buildings with identical heat pumps all in a field together, but not so close that they can affect each other. By some freak of nature, the weather and OAT stay constant all the time, the OAT being 5 degrees. In the first building, the heat pump maintains the IAT at a steady average of 20 degrees over a day. In the second building, the heat pump maintains a steady average IAT of 10 degrees over a day. Now, I think we would all agree that the second building will use less energy that the first building. But what about the third building, which maintains an average IAT of 15 degrees, with that average coming about because it has a 12 hour period of 10 degrees, followed by a 12 hour period of 20 degrees. How much energy will it use, compared to the other two?

The general question is whether a building with a lower overall average IAT must, all other things being the same, always use less energy than a building with a higher overall average IAT? And then, if the answer is yes, does it not follow that the same building, when running with a setback as compared to no setback, must use less energy, because its overall average IAT is lower?        

You required a modeling tool to answer the questions.

IAT           10           Avg. 15              20

PI          10644         74262            55484

COP         5.64            2.84               3.24

PO         60030        211217           179968

LWT       21.28        21.14 / 55         42.9

IAT          10            10 / 19.37        20

There's no need to thank me.

Posted by: @derek-m

↑

Posted by: @jamespa

↑

Posted by: @derek-m

↑

Table 1 was primarily to illustrate that without recovery boost it may not be possible to fully recover IAT. My calculation of energy saving would be given by 4819/26893 = 17.92%.

Thanks for the explanation, just one supplementary, should we infer from the quote above that you don't consider this a valid scenario in answer to the question posed?

 

James

I was merely stating that without some form of recovery boost, the time required for IAT to reach the desired value may be lengthy. A further determining factor is the size of boost and the period over which it is supplied. Just as with the 'slow and low' continuous running regime, a longer slower boost should provide greater energy saving. At the end of the day it is for individual heat pump owners to find out what works best for them, taking all considerations into account.

 

Thanks. My concern is that the less engaged may take the example as indicative of what is achievable in terms of saving, whereas it is not since the house is not returned to the same state in which it started.  I think you, I and @cathoderay, who have been following the thread closely understand this, but others who dip in may not.  Anyway I believe I understand what it is intended to show.

Thank you for your explanation of the derivation of the formulae.  My gut feel is that, unless I can think of a neat way to write custom formulae for cop(ft, oat, power, range), max_output(ft, oat, range), min_output(ft, oat, range) (range being the cell range containing the manufacturer data in a form which is recognisably derived from the way the manufacturer presents it), then it's unlikely that it's possible to improve the readability substantially.  The main problem is the first of these, which requires 3 d interpolation and somehow a formula which processes the tables for power in the slightly awkward way they are typically presented.  However if this can be cracked with a reasonably simple piece of code, then it would massively aid readability and relatively easy development of ever more useful models.  I will continue to think about it.

Finally @cathoderay, @derek-m is there any chance of a ceasefire?  I think this exercise has shown that we are all fallible and can all learn from each other, that both experimental and theoretical determination of what we are all trying to find out is extremely challenging indeed (perhaps more so than any of us initially thought) and hints that we maybe need a bit of both (or a dedicated heat pump lab which we sadly lack) if we are to crack this vital topic.  Doubtless professional experimental and theoretical physicists have similar disagreements, but I think we would all have to acknowledge that science and engineering generally progress based on a combination of the two. 

Personally  I don't think any interpretation of experimental results can be trusted unless it can be rationalised theoretically, and equally no theory can be trusted unless tested by experiment!  This needs to be a collaboration not a competition.  Just offering my opinion, please feel free to ignore.

@jamespa

I can assure you that I was not being combative, merely having some fun, otherwise I would have given my usual warning 'that I don't take prisoners'.

Whilst I am reasonably confident that the modeling tool performs in a similar manner to a heat pump running in a constant manner, exactly what happens during cycling may not be fully replicated. Also defrosting cannot be accurately replicated by the modeling tool other than making some sort of allowance dependent upon OAT values.

I suppose the next objective would be to obtain some reasonably accurate data from a running system, which could then be fed into the modeling tool to test its accuracy. Unfortunately I have an A2A heat pump, that does not provide the necessary data.

Posted by: @derek-m

↑

Whilst I am reasonably confident that the modeling tool performs in a similar manner to a heat pump running in a constant manner, exactly what happens during cycling may not be fully replicated. Also defrosting cannot be accurately replicated by the modeling tool other than making some sort of allowance dependent upon OAT values.

I tend to agree with all of that.  Cycling in particular is a separate and interesting problem which currently (a bit like setback) is the subject of folklore not fact.  However it's probably too ambitious to expect to model it beyond the pure thermodynamics, because the rest is engineering detail in the compressor and other components about which reliable information is almost non-existent.

Heat pump manufacturers cop data frequently purport to include the effects of defrost.  However whether the reference humidity they use is typical of the UK or central Europe appears unclear.  I suspect this makes a material difference.

Posted by: @jamespa

↑

Personally I don't think any interpretation of experimental results can be trusted unless it can be rationalised theoretically, and equally no theory can be trusted unless tested by experiment! 

By and large I agree, but I don't give the two (experiment and theory) equal weight. Given accurate enough experimental data, it always trumps theory, when experiment and theory disagree. In practice you must bend the theory to fit the data, not the data to fit the theory. The same principle is at work in Sherlock Holmes's "when you have eliminated the impossible, whatever remains, however improbable, must be the truth".

Moving on...

Posted by: @derek-m

↑

I suppose the next objective would be to obtain some reasonably accurate data from a running system, which could then be fed into the modeling tool to test its accuracy.

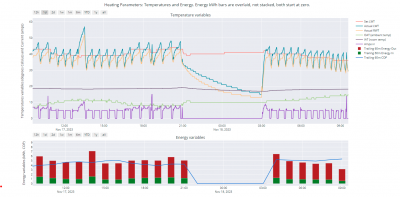
We do have data - mine, and so far as we know, it is reasonably accurate. At least it is as accurate as the accuracy with which Midea measures the data. Here is the last 24 hours data from a running system. behind every point line and bar on that chart is hard data which I am more than happy to post here:

My data comes from a Midea heat pump, which means the spreadsheet would have to be copied and the copy modified to have Midea data, but we also have @kev-m's charts, and if memory serves, he has an Ecodan heat pump. If he is able and willing to post his underlying data, along with the necessary 'initial data' (heat loss etc), then all you need to do is put his numbers into your spreadsheet, and compare the spreadsheet predictions to the actual data.